| On
le savait capable de jouer de la musique, il était même devenu un instrument
à part entière en 20 ans de musiques électroniques. Mais l'ordinateur
pouvait-il « écouter » de la musique ? Pouvait-il battre la mesure, reconnaître
les notes, nommer les instruments ? Des chercheurs travaillent aujourd'hui
pour doter les machines numériques de ces nouvelles possibilités.
Vous avez sans
doute déjà échangé ou téléchargé
des fichiers musicaux sur votre iPod ou votre ordinateur. Vous n’êtes
pas les seuls ! Vous êtes même si nombreux qu’il est
devenu impossible de conseiller chacun individuellement sur la toile ou
de ranger manuellement chacun des morceaux avec ceux du même style
par exemple. Mais la prochaine révolution de la recherche sur Internet
tient probablement dans notre mode de communication avec la toile. Aujourd’hui
de nature essentiellement textuelle -nous tapons du texte dans l’invite
des moteurs de recherche- son avenir s’ouvre à un butinage
électronique multimodal, faisant intervenir l’audio, l’image
et la vidéo. C’est pourquoi, depuis maintenant une quinzaine
d’années, un nouveau domaine de recherche a émergé,
qui vise à doter l’ordinateur de capacités à
analyser automatiquement la musique.
La musique
organise une suite de sons pour créer des attentes, produire un
sens émotionnel. Les ressorts sous-jacents sont multiples et font
intervenir à la fois nos sens (audition), notre mémoire
et notre cognition. Il serait probablement très ambitieux de s’attaquer
à tous ces aspects et notre objectif, plus modeste, est d’essayer
de reproduire au mieux, à l’aide d’algorithmes numériques,
certaines des capacités humaines d’appréhension de
la musique. Nous parlerons ici de deux dimensions de compréhension
du message musical : celle de battre du pied, de danser ou de claquer
des doigts en rythme avec un morceau et celle de reconnaître des
notes, isolées ou simultanées.
Rythme
et battue.
La position temporelle des évènements rythmiques et leur
durée constituent le matériau de base de notre analyse du
rythme. Sur une partition, ces deux éléments sont explicités
: les codes du solfège traditionnel par exemple (noire, croche,
blanche, soupir, etc…) permettent de les préciser de manière
univoque. Une structuration usuelle de ce contenu rythmique d’une
pièce musicale fait apparaître plusieurs niveaux de hiérarchie
: la plus petite unité de durée séparant deux évènements
consécutifs (tatum), le niveau de l’unité temporelle
comme la noire par exemple, ou encore la battue (tactus) et un niveau
plus élevé qui découpe le flux musical en segments
comme la mesure. Ici nous allons nous limiter au niveau intermédiaire.
Nous allons décrire les principes qui permettent de programmer
l’ordinateur pour qu’il batte, synchronisé avec la
musique.
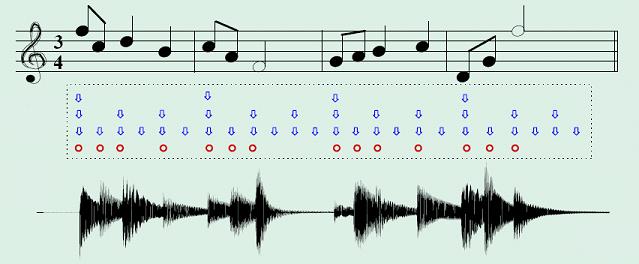
Imaginons d’abord
un cas simple, celui d’un tic-tac régulier (un métronome
ou un claquement de main). Une fois enregistré à l’aide
d’une carte son, le signal obtenu a la forme donné sur la
figure suivante.
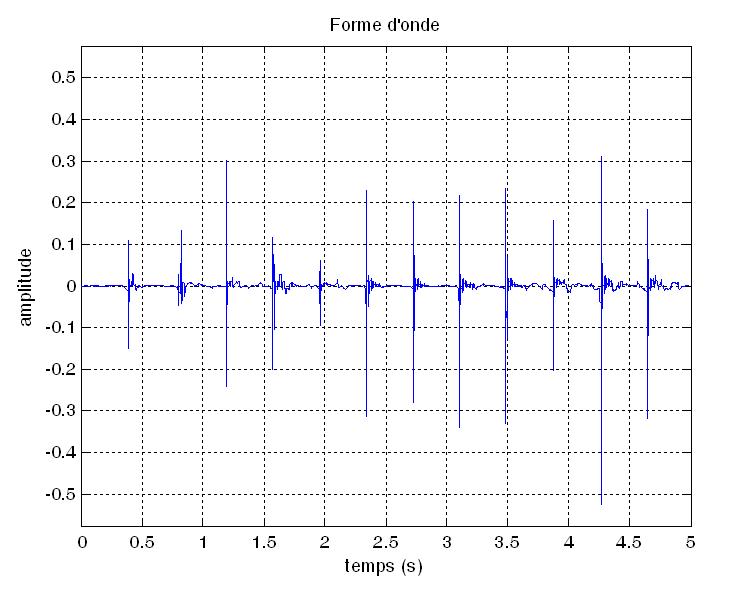
Dans ce cas, nous allons très simplement essayer de (1) détecter
la position des évènements, (2) d’estimer leur régularité
(fréquence ou période d’horloge) puis (3) de synchroniser
notre propre battue —ici un bip généré par
l’ordinateur— avec le signal d’origine.
Détection
de la position des évènements.
Regardons de plus près l’un des évènements
qui sont ici des claquements de mains.
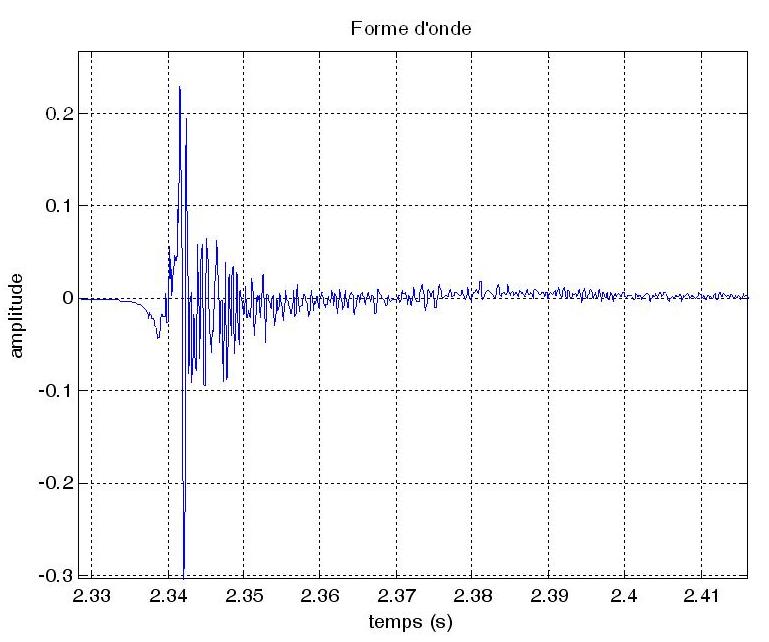
Nous voyons que la forme d’onde enregistrée par le micro
présente une forte variabilité. Pour notre tâche seule
nous importe l’allure générale, ce que nous appelons
couramment l’enveloppe du signal, qui décrit les variations
grossières de l’énergie du signal. Intuitivement :
l’enveloppe monte quand le signal devient plus fort et décroît
dans le cas contraire. En traitement du signal, nous savons concevoir
des détecteurs d’enveloppe, capables de produire une telle
enveloppe.
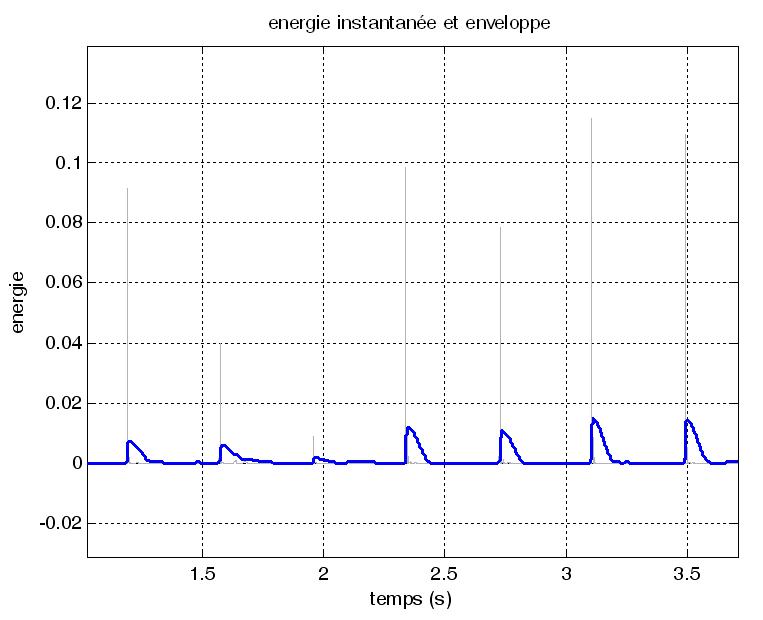
Comme vous
pouvez le remarquer sur la figure précédente l’enveloppe
que nous avons calculée suit bien les montées énergétiques
mais mal les baisses d’énergie. Ceci n’est pas une
erreur d’algorithme mais résulte d’une volonté
délibérée de correspondre au fonctionnement de notre
système auditif, qui réalise ce type d’intégration
temporelle de l’énergie. On pourrait dire qu’après
un bruit impulsionnel, notre oreille devient en quelque sorte moins sensible,
pendant un court laps de temps, à une nouvelle sollicitation.
Pour détecter
les fronts montants de cette enveloppe, qui sont précisément
localisés à l’endroit du début des évènements,
encore appelés attaques, on utilise une mesure du taux de variation
de cette enveloppe. Ce taux va être grand quand l’enveloppe
varie vite, c’est à dire au niveau des attaque et va être
négatif lorsque l’enveloppe décroît.
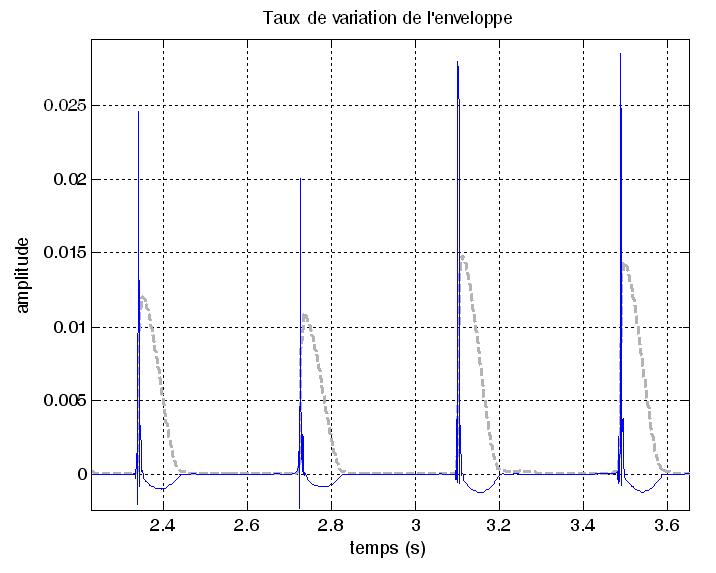
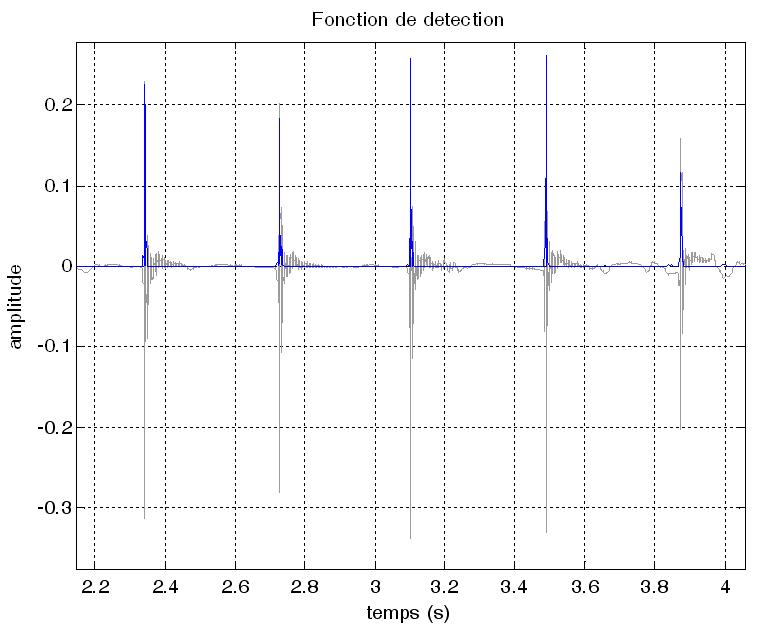
C’est pourquoi nous ne conserverons que la partie positive. Le résultat,
appliqué à l’ensemble de l’extrait, produit
une courbe qui met en avant la position temporelle de début des
évènements. Une telle courbe est appelée fonction
de détection et son calcul permet d’apprécier la régularité
temporelle du signal. Elle est représentée ci-dessous, en
superposition de la forme d’onde originale.
Mesure
de régularité.
Pour connaître
maintenant plus précisément la régularité
nous allons devoir la mesurer. Ceci peut-être réalisé
de plusieurs manières mais nous avons ici choisi d’utiliser
une fonction d’autocorrélation qui mesure en quelque sorte,
le taux de ressemblance d’un signal à lui-même lorsqu’on
le décale. Lorsque le signal est périodique on comprend
que ce taux est maximal pour un décalage égal à une
(ou 2 ou 3 etc…) période. Une simple détection du
premier pic maximum permet alors de trouver la période.
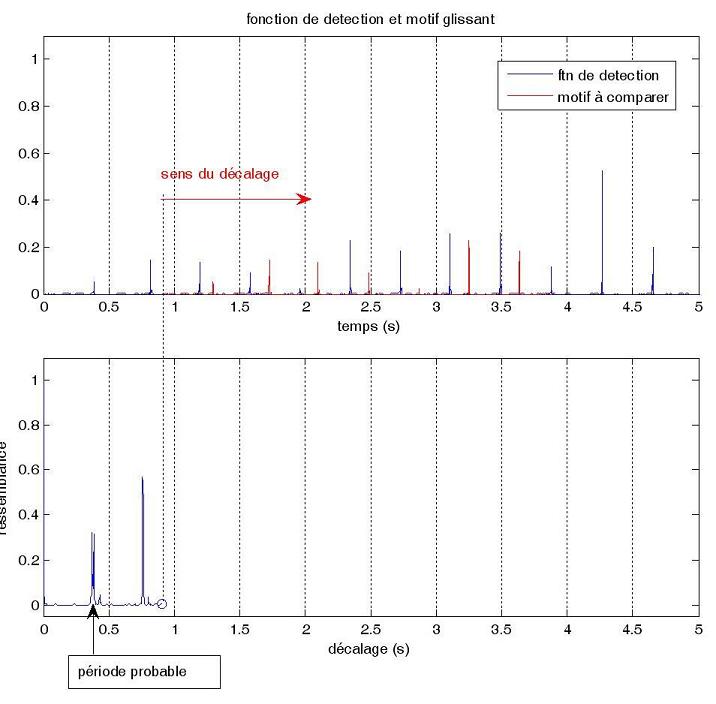
Ici on trouve un période probable autour de 0.4s soit une cadence
de 60/0.4 = 150 battements par minutes (bpm).
Synchronisation
avec une horloge synthétique.
Nous connaissons maintenant la cadence de notre battue et la dernière
étape consiste à la synchroniser avec le signal. Pour cela
nous allons comparer un train d’impulsion à la cadence trouvée
de 150 bpm et la fonction de détection obtenue plus haut pour voir
le moment où les deux sont le plus en phase. On calcule pour cela
la fonction d’intercorrélation qui sera maximum à
l’instant précis où cette mise en phase est la meilleure.
Cas
d’un morceau de musique.
Passons maintenant à un cas plus compliqué, celui d’un
morceau de musique. De nombreux instruments sont impliqués et les
évènements peuvent être des bruits impulsionnels lorsque
des instruments de percussion jouent ou sont des notes jouées par
des instruments mélodiques (le piano, la trompette, le violon,
etc…). La méthode précédente ne s’applique
pas car dans de nombreux cas, les évènements se recouvrent
et alors l’énergie des plus fort l’emporte alors que
ce ne sont pas nécessairement les plus significatifs dans notre
perception du rythme. La solution consiste alors à découper
d’abord le signal en bandes de fréquence disjointes, comme
par exemple grave/médiums/aiguës. Simplement ici on utilisera
plus que 3 bandes en général.
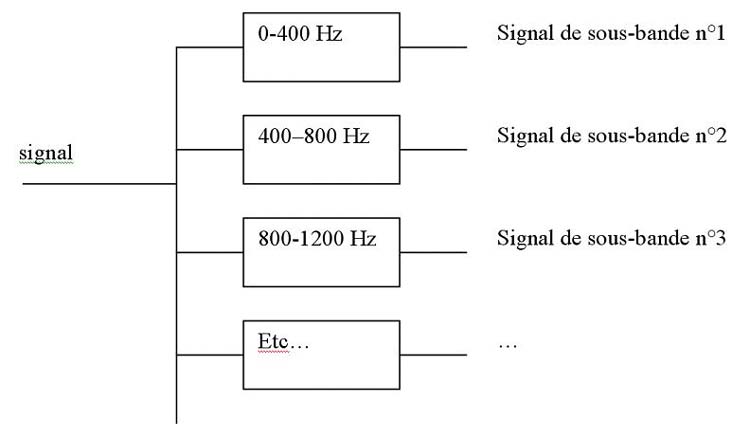
Ensuite le traitement précédent est appliqué : détection
d’enveloppe + mesure de régularité pour chacune des
bandes. La régularité la plus marquée lorsqu’on
considère l’ensemble des bandes sera prise comme résultat
final. La mise en phase se fait par mise en phase du signal d’horloge
et du morceau de musique.
Exemple
: jazz (Brad Melhdau)
Transcription
et mélodie.
De même que pour le rythme, les codes du solfège traditionnel
permettent de représenter le contenu musical en termes de contenu
harmonique et mélodique, c'est-à-dire de représenter
les évènements musicaux sous forme de notes. Chaque note
est caractérisée par sa hauteur qui peut être mesurée
en Hertz (Hz) même si les musiciens associent plus facilement des
noms (do, ré, mi,…) à ces hauteurs. On pense ici naturellement
au La du diapason, souvent appelé « La 440 », qui effectivement
correspond à un son dont la fréquence fondamentale est de
440 Hz. Les sons musicaux qui ont une hauteur sont périodiques
et la hauteur perçue est, dans la majorité des cas, directement
liée à cette période. Ainsi, pour mesurer ou estimer
la hauteur d’une note il est essentiel de pouvoir estimer la période
fondamentale (ou inversement fréquence fondamentale) de la note
produite similairement à la mesure de période effectuée
pour l’estimation du tempo :
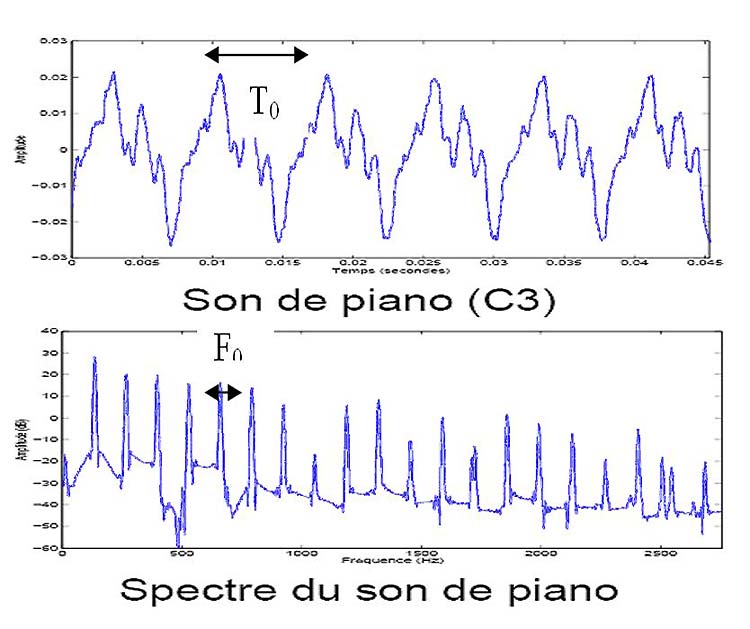
Figure : La période fondamentale est représentée
par le temps T0. La fréquence fondamentale F0 (avec F0=1/T0) peut
se mesurer de deux façon sur le spectre.
On peut mesurer la hauteur aussi bien en s’appuyant sur les propriétés
temporelles du signal (par exemple grâce à son autocorrélation
comme pour le rythme) ou de manière équivalente sur le spectre
en remarquant que le son de hauteur 130 Hz aura des « pics »
de fréquences (on parlera ici d’harmoniques) aux différents
multiples de 130 Hz. On peut ainsi localiser la position du premier pic
(correspondant à la fréquence fondamentale), mais comme
celui-ci n’est pas toujours présent on pourra aussi mesurer
l’écart moyen entre chaque pic. Les accordeurs électroniques
que les musiciens connaissent bien fonctionnent suivent l’un de
ces deux principes pour indiquer si la note produite est juste par rapport
à sa hauteur théorique.
Le problème
devient beaucoup plus difficile lorsqu’il y a plus d’une note…Le
musicien exercé pourra pour déterminer quelles notes ont
été jouées dans un accord en focalisant son attention
sur chaque note à tour de rôle….en faisant cela, il
fait une sorte de séparation des différentes voix (en traitement
de signal on parle ici souvent de « séparation de sources
»). C’est le principe de base que va essayer de suivre l’ordinateur
: il va d’abord estimer la hauteur de la note prépondérante,
puis soustraire cette note de l’accord et estimer la note suivante
et ce processus sera répété tant qu’il reste
des notes dans l’accord.
Les illustrations suivantes détaillent ces étapes sur un
accord de 2 notes Do, Fa#.
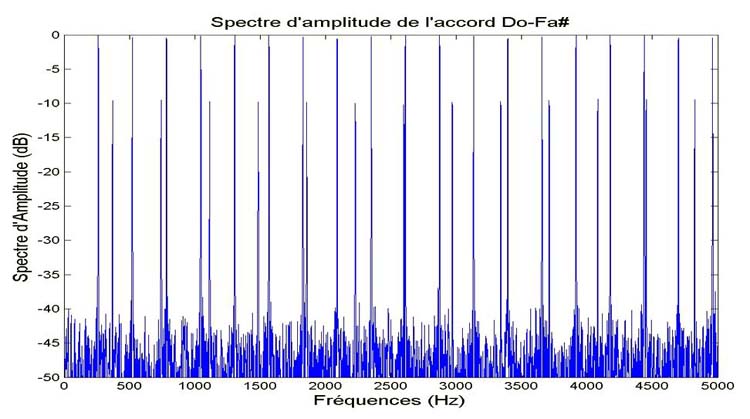
Figure : Spectre d’amplitude d’un accord de 2 sons synthétiques
(notes do et Fa# avec un peu de bruit de fond.)
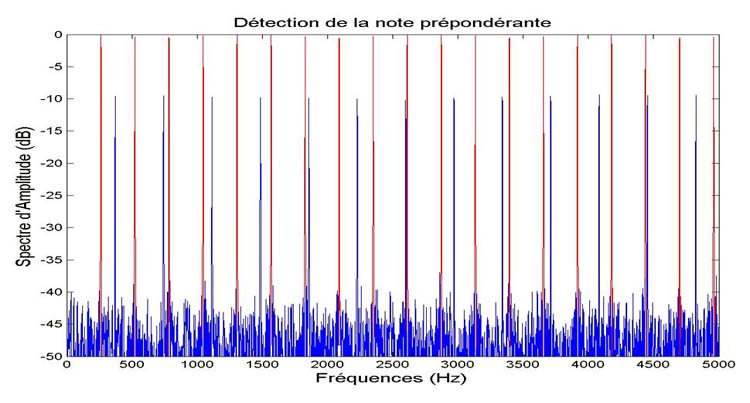
Figure : Détection de la note prépondérante (le do
d’une fréquence fondamentale de 261 Hz). Les pics fréquentiels
correspondant à cette note sont marqués en rouge.
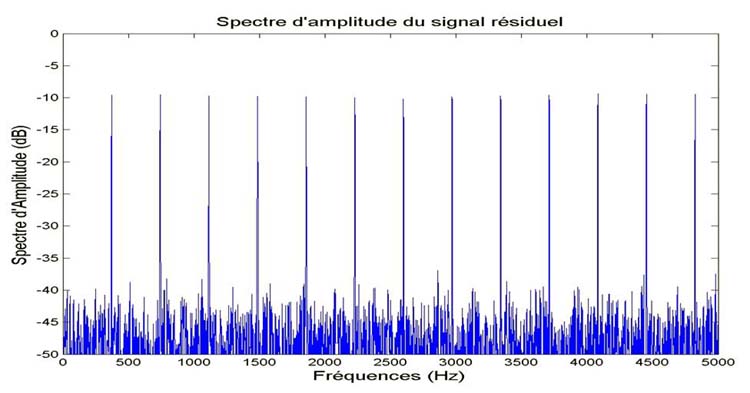
Figure : Spectre du son résiduel avec suppression du do
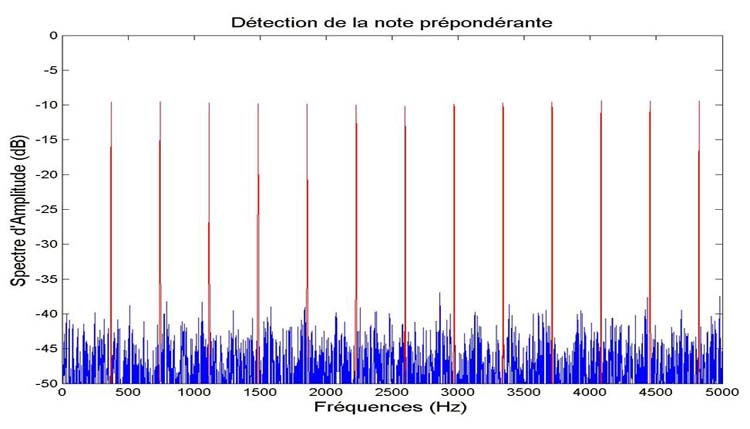
Figure : Détection de la note prépondérante (le Fa#
d’une fréquence fondamentale de 371 Hz). Les pics fréquentiels
correspondant à cette note sont marqués en rouge.
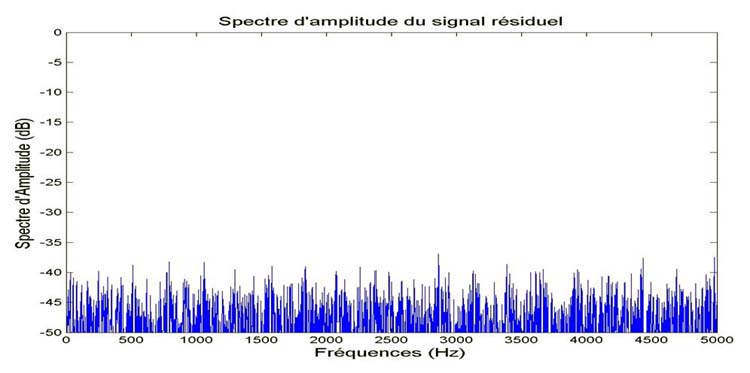
Figure : Spectre du son résiduel avec suppression du Fa# : il ne
reste plus de notes
On peut maintenant
faire une telle analyse en l’associant avec la détection
du rythme sur tout un morceau. On obtiendra ainsi une forme de partition
correspondant au morceau analysé sous la forme de « piano
roll » à l’image des partitions de carton perforés
des orgues de barbarie ou autres automatophones.
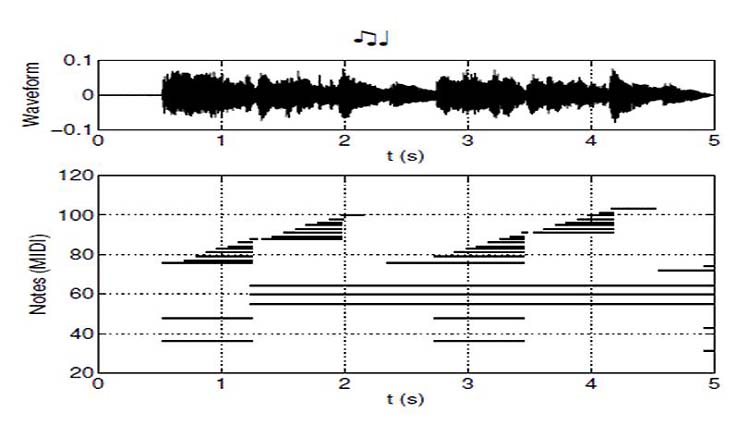
Figure : Image de piano roll : En haut, on reconnait la représentation
temporelle du signal et en bas la représentation sous forme de
«pianos roll » (ou cartons perforés). Chaque trait
noir correspond à une note jouée pendant une durée
proportionelle à la longueur du trait.
Il est possible
de vouloir extraire ou connaître la succession des notes d’une
des voix d’un enregistrement musical et ce en particulier celle
qui correspond à la mélodie principale. En effet, la mélodie
est souvent indissociable d’une œuvre et la connaissance de
cette mélodie ouvre des perspective nombreuses d’utilisation
par l’ordinateur : recherche de morceaux par chantonnement d’un
bout de mélodie, contrôle des droits d’auteurs sur
l’originalité d’une nouvelle mélodie, suppression
de la mélodie pour la karaoké, etc…
Si l’humain
a des facultés naturelles pour reconnaître une mélodie,
l’ordinateur est encore limité mais comme on le verra il
parvient dans certains cas à des résultats tout à
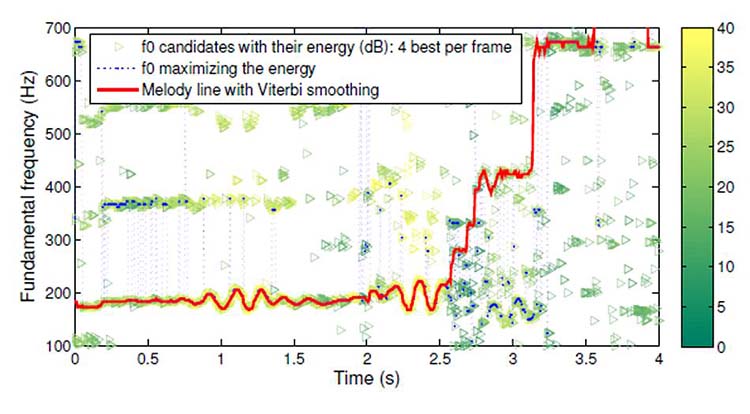
fait intéressants. Pour y parvenir, l’ordinateur fera des
suppositions sur les traits caractéristiques d’une mélodie
: il supposera par exemple que les notes successives d’une mélodie
ne sont jamais trop éloignées en fréquences les unes
des autres ni trop différentes en énergie…L’ordinateur
va ainsi traquer dans la succession des notes trouvées, la suite
de notes parmi les plus énergétiques, qui correspondent
à un timbre proche et qui forment une ligne mélodique souple.
Une fois les
notes de la mélodie trouvées, il est alors possible de les
supprimer du signal musical et de générer un accompagnement
seul ou la voix seule autorisant d’innombrables possibilités
de nouveau mixage (somme pondérée).
Pour écouter
les sons correspondants et bien d’autres, se connecter à
http://www.tsi.enst.fr/~durrieu/en/icassp09/
(séparation de voix principale, thèse de J-L. Durrieu)
http://perso.telecom-paristech.fr/~emiya/
(transcription automatique de piano, thèse de V. Emiya)
VIDEO de la conférence
Audio, Acoustique et Ondes
Telecom ParisTech Paris
|



