Lundi 12 Février 2007

Comment le magnétisme vient aux molécules

Michel Verdaguer
Françoise Villain

Université Paris VI

Comment le magnétisme vient aux molécules
… et le monde merveilleux qui en résulte

Le mot magnétisme, utilisé dans la vie de tous les jours, évoque généralement des matériaux solides, métaux, alliages, oxydes. Les molécules sont elles, le plus souvent considérées comme des objets isolés, non magnétiques. Pourtant, être ou ne pas être (magnétique) n’est pas la vraie question : tout est magnétique. Le vrai problème est de savoir comment. Cet exposé propose d’illustrer le magnétisme des molécules à partir de quelques expériences,

Du magnétisme des aimants à celui de la molécule
Dans la vie quotidienne, les corps que l’on appelle « aimants » peuvent être classés en deux catégories : les aimants « durs » et les aimants « doux ». Les aimants durs restent aimantés en permanence (« aimantation rémanente » importante) et peuvent attirer à eux les aimants doux qui perdent ensuite rapidement leur aimantation (« aimantation rémanente » faible ou nulle). Les aimants durs (alliage neodyme-fer-bore par exemple) créent autour d’eux un champ magnétíque qu’on peut visualiser à l’aide de matériaux doux (expérience des lignes de flux magnétique de M. Faraday, Figure 1).

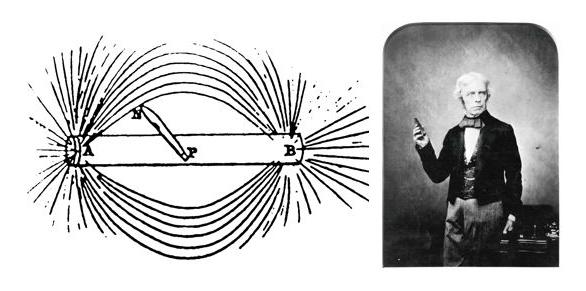
Figure 1 : Première illustration des lignes de champ magnétique autour d’un aimant permanent, matérialisées par de la limaille de fer (1832) ; Michael Faraday tenant un aimant.
(communication privée, P. Day et F. James, Royal Institution, Londres).[Voir aussi : P. Day, The Philosopher’s Tree,The Institute of Physics Publishing, Bristol, 1999]

Le fait que le champ magnétique ne soit pas visible, que les interactions magnétiques s’exercent à distance, sans contact direct, comme l’illustrent les expériences très populaires de lévitation (figure 2), peuvent être utilisés de manière mercantile et abusive par des charlatans. La théorie du « magnétisme animal » de Messmer, auquel Mozart fait allusion dans la scène IV de Cosi Fan Tutte (« pietra mesmerica ») a fait bien des victimes trop crédules avant que son créateur ne se retrouve en geôle pour escroquerie. Dans le langage quotidien, le charme et le charisme de certaines personnes, de leurs yeux notamment, est souvent qualifié de « magnétique » : Fernande Olivier, l’une des premières compagnes de Picasso, confesse que le 4 août 1904 … « Ce rayonnement, ce feu intérieur que l’on sentait en lui, dégageaient une espèce de magnétisme à quoi je ne résistai pas … ». Les exemples abondent.

Figure 2 : Corps en lévitation : une toupie en rotation à gauche, un globe terrestre à droite lévitent. Leur poids est exactement opposé à la force magnétique exercée par des aimants sur la substance aimantée dont ils sont constitués. L’interaction s’exerce sans contact direct et lui confère indûment un caractère étrange et « magique ».

L’utilisation la plus connue et l’une des plus utiles du magnétisme, – elle a servi notamment dans la panoplie des instruments de navigation qui au XVe siècle ont permis les grandes découvertes, en Espagne, au Portugal, en Chine … - est évidemment la boussole dont l’aiguille s’oriente dans le champ magnétique terrestre dû lui-même aux masses métalliques du noyau terrestre (figure 3). Inventée en Chine, la boussole a été mise en boîte par les Italiens de la côte amalfitaine, d’où son nom (bussola en italien = petite boite). Les jouets magnétiques suscitent souvent les passions enfantines (figure 4).

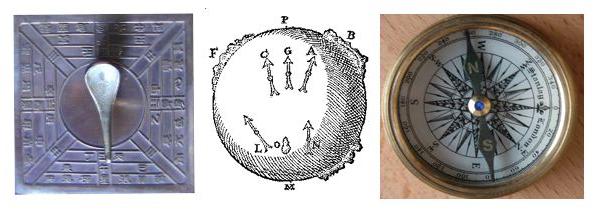
Figure 3 : une application bien connue du magnétisme, la boussole : du modèle Si Nan du musée d’histoire de Beijing à la terrella de William Gilbert (de Magnete, 1600) et à une boussole moderne de collection.

Figure 4 : les jeux de construction à base d’éléments magnétiques n’engendrent pas la mélancolie des jeunes enfants.

Les « magnets » qui ornent bien des portes de réfrigérateurs et de tableaux d’affichage ne sont pas moins répandus. Aimants durs et aimants doux occupent une part considérable dans le fonctionnement des moteurs de véhicules automobiles, les transformateurs, etc …
Une grandeur particulièrement importante pour caractériser les matériaux magnétiques est la température dite de Curie (Tc), mise en évidence par Pierre Curie, qui indique la température de passage d’un état magnétique ordonné à longue distance à un état désordonné. L’expérience dite du clou (la température de Curie du fer est de 770º Celsius), consiste à chauffer un clou de fer suspendu à un pendule, jusqu’à ce qu’il ne soit plus attiré par un aimant (à la température de Curie). Elle peut être réalisée plus aisément avec un matériau dont la température de Curie est proche de la température ambiante. En effet, certains matériaux moléculaires aimantés deviennent paramagnétiques par simple chauffage par un rayon lumineux (figure 5).

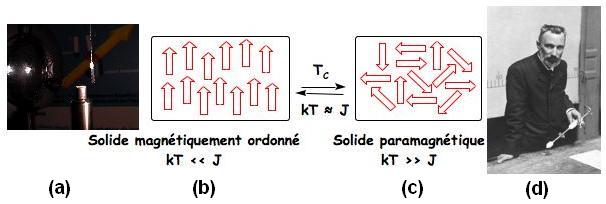
Figure 5 : Température de Curie : (a) expérience du « clou » ; au centre, modélisation du passage d’un solide magnétique désordonné (c) à un solide magnétiquement ordonné (b) quand l’interaction entre moments magnétiques devient du même ordre de grandeur que l’agitation thermique ; (d) Pierre Curie réalisant des expériences dans l’amphithéâtre de Physique, 12 rue Cuvier (origine du cliché : musée Curie, Paris).

Lorsque l’on examine un aimant, on peut observer qu’il est constitué de « domaines » magnétiques » eux-mêmes constitués de nombreux moments magnétiques, le stade ultime étant le moment magnétique porté par un seul atome ou une seule molécule (figure 6).

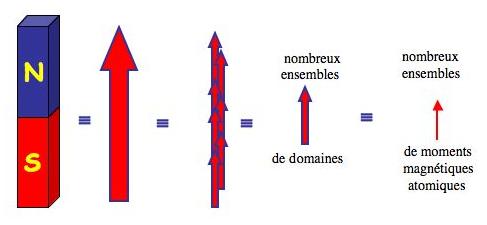
Figure 6 : Schéma de décomposition d’un aimant en domaines et en moments magnétiques ;

Lorsqu’on applique un champ magnétique sur un aimant, on peut changer la direction de l’aimantation (la manière dont le matériau s’aimante), jusqu’à la renverser. Le renversement de l’aimantation affecte de manière différente les divers domaines. La courbe qui donne l’aimantation en fonction du champ appliqué comporte le plus souvent un cycle d’hystérésis lors du balayage du champ de fortes valeurs positives à de fortes valeurs négatives (Figure 7). Le cycle d’hystérésis dépend énormément du système comme le montre la figure 7.

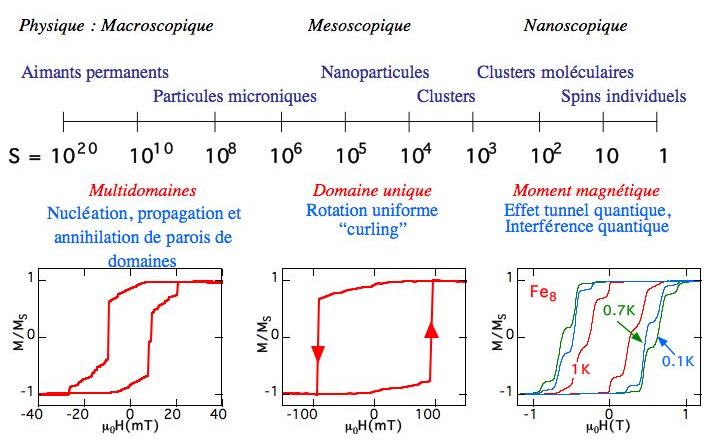
Figure 7 : de la physique macroscopique à la physique nanoscopique, de la physique des domaines à la physique quantique (adapté de W. Wernsdorfer, I.L. Néel, Grenoble) : la variation de l’aimantation en fonction du champ magnétique appliqué présente un cycle d’hystérésis dont la nature est complètement différente selon la taille des moments magnétiques. Le magnétisme de la molécule (à droite) est dominé par les phénomènes quantiques.

Tout cela participe du magnétisme dit « classique », macroscopique, à notre échelle avec d’innombrables applications utiles. Pour le commun des mortels, les molécules quant à elles n’entrent pas dans cette catégorie « magnétique ». Pourtant, l’air que nous respirons à chaque instant consiste essentiellement en un mélange de molécules de diazote, N₂ et de dioxygène, O₂ (chaque molécule est constituée de deux atomes d’azote N ou d’oxygène O). Ces molécules sont «magnétiques», chacune à leur manière. Les molécules de diazote sont «diamagnétiques» : placées dans un champ magnétique intense elles sont très faiblement repoussées. Les molécules de dioxygène sont «paramagnétiques» : placées dans un champ magnétique puissant elles sont faiblement attirées. Nous expliquerons ces propriétés dans un instant, mais l’expérience permet de les illustrer simplement : on plonge un aimant en U dans du diazote liquide (a) ou dans du dioxygène liquide (b, c) et l’on obtient les résultats de la figure 8.

Figure 8 : Propriétés magnétiques des molécules composant l’air : a) le diazote liquide, diamagnétique, ne se fixe pas sur les pôles de l’aimant permanent ; b) le dioxygène liquide, paramagnétique, est attiré par les pôles de l’aimant, il forme un cylindre liquide entre les deux pôles ; c) à la température ambiante, le dioxygène liquide s’évapore et le liquide restant est attiré par l’un et l’autre pôle.
(montage réalisé par S. Gao, université de Beijing).

Le monde quantique
Dans tous les cas, solide, liquide ou molécule, le magnétisme trouve son origine dans les propriétés magnétiques de l’électron. Et l’on passe ici du monde macroscopique au monde quantique, un monde très particulier, découvert à la fin du XIXe siècle et au début du XXe siècle et célébré récemment lors de l’année mondiale de la physique 2005. Ce monde est quantifié ; la discontinuité s’y substitue à la continuité du monde macroscopique. C’est un monde aux règles bien établies, régi par des nombres quantiques et des fonctions mathématiques qui dépendent de ces nombres … C’est un monde où les dimensions deviennent toutes petites, où le nanomètre (= 10^-9 mètre = 1 mètre / 1000 000 000) remplace le mètre, où la quantité de matière devient extrêmement faible, un monde où la molécule se substitue à la mole (une mole de molécules est constituée de 6,023 10⁺²³ molécules, i.e. la constante d’Avogadro, un nombre difficilement imaginable obtenu en multipliant vingt trois fois 10 par lui-même …). C’est aussi un monde dont les concepts sont difficiles à appréhender simplement mais qu’il est possible d’approcher par des analogies, des modèles, des représentations … C’est un monde que l’on peut considérer comme merveilleux, plus merveilleux encore que le monde qu’Alice découvre aux pays des merveilles.

L’électron et ses propriétés magnétiques dans l’atome
L’électron présente de multiples visages : c’est d’abord un corpuscule ayant une masse élémentaire, une charge élémentaire négative, un moment magnétique élémentaire (le magnéton de Bohr) ; c’est aussi une onde, décrite par une fonction mathématique appelée fonction d’onde, solution d’une équation proposée par Erwin Schrödinger, l’équation de Schrödinger. Dans un atome, où les électrons à charge négative « tournent » autour du noyau chargé positivement, à chaque fonction d’onde ou orbitale, est associée une énergie correspondant à un état stationnaire de l’atome. C’est l’une des premières merveilles du monde quantique qui permet à deux charges de signe opposé de coexister de manière stable au lieu de se précipiter l’une sur l’autre comme dans notre monde classique … L’existence de l’atome stable est fondée sur cette propriété.
La description quantique de l’électron repose sur quatre nombres qui quantifient ses propriétés. L’année de la physique 2005 a popularisé ces notions et nous n’y revenons pas. Le nombre quantique de spin est égal à s = ½. Le moment magnétique correspondant – qu’il est commode d’associer à un mouvement de rotation du spin sur lui-même dans un sens ou dans le sens opposé (to spin signifie tourner sur soi-même, en anglais) - est orienté vers le haut (up, ) pour ms = + ½ ou vers le bas (down,), ms = - ½. En première approximation, on peut considérer que ce moment est égal au magnéton de Bohr, µ_B.
Pour « occuper » les orbitales, la mécanique quantique a un ensemble de règles qu’on peut essayer d’exprimer simplement : pas plus de deux électrons par orbitale (principe de Pauli) et quand il y a deux électrons, ils sont de moments magnétiques opposés. C’est une paire d’électrons (figure 9).

Figure 9 : Occupation d’une orbitale atomique par les électrons :
niveau simplement occupé, « up » pour ms = + ½ , « down » pour ms = - ½ et niveau doublement occupé.

Les niveaux d’énergie correspondant aux orbitales se peuplent à partir des niveaux les plus stables (principe de construction, on commence toujours par le bas !). Quand plusieurs niveaux ont même énergie, l’état qui est le plus stable est celui de plus haut spin dit le principe de Hund (figure 10). Ce phénomène est dû ici à l’orthogonalité des orbitales. Leur recouvrement, définie par une intégrale mathématique, est strictement nul.

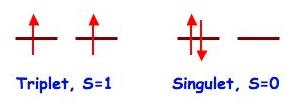
Figure 10 : comment deux électrons occupent-ils deux orbitales orthogonales (qui ne se recouvrent pas) de même énergie ? Le principe de Hund répond que l’état le plus stable est l’état de plus haut spin, le triplet, S=1.

Nous oublions dans cette approche très simplifiée à la fois le magnétisme dû au mouvement orbital des électrons autour du noyau et le magnétisme du noyau lui-même, pourtant si important en imagerie médicale.

Les électrons dans les molécules
Une molécule est l’assemblage de plusieurs atomes. Les fonctions d’onde décrivant les électrons dans les molécules peuvent être représentées comme des combinaisons linéaires d’orbitales atomiques (OA). Ce sont les orbitales moléculaires (OM). Il y a autant d’orbitales moléculaires que d’orbitales atomiques initiales …). Et les règles d’occupation par les électrons sont les mêmes.
Molécule de dihydrogène et de diazote (diamagnétiques) et de dioxygène (paramagnétique)
La molécule de dihydrogène est constituée de deux atomes d’hydrogène dont les orbitales se combinent en phase et en opposition de phase avec un recouvrement axial () pour donner deux orbitales moléculaires (figure 11). Les deux électrons s’apparient up et down, dans l’orbitale la plus basse en énergie. La molécule est diamagnétique.

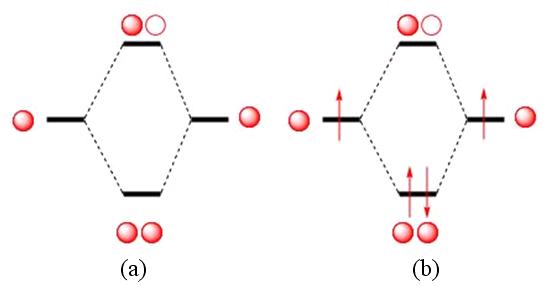
Figure 11 : Formation d’une molécule de dihydrogène : (a) combinaison des orbitales atomiques ;
(b) appariement des spins dans l’orbitale moléculaire stable, « liante ».

La molécule de diazote est également diamagnétique. Tous ses électrons sont appariés comme le montre la figure 12 pour les orbitales moléculaires formées par recouvrement latéral des orbitales p (). L’occupation des quatre orbitales moléculaires de molécules analogues (figure 12) permet aussi de démontrer le paramagnétisme du monoxyde d’azote (c) (spin = ½), du dioxygène avec deux électrons célibataires dans deux orbitales orthogonales, suivant le principe de Hund (d) (S = 1, triplet). Ces schémas d’orbitales moléculaires expliquent simplement les propriétés magnétiques du diazote et du dioxygène (montrées expérimentalement en figure 8).

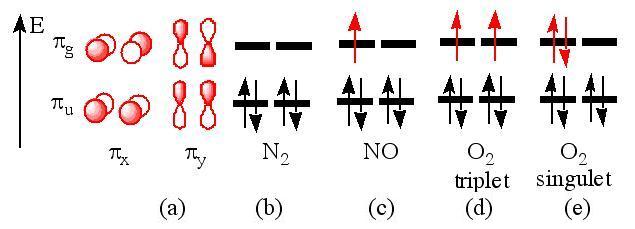
Figure 12 : Occupation des orbitales dites 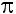(a);
du diazote (b); du monoxyde d’azote (c) ;du dioxygène triplet (d) ; du dioxygène singulet (e).

Cette situation nous conduit à une observation d’intérêt très général. L’air que nous respirons est essentiellement constitué de molécules de diazote et de molécules de dioxygène. Le diazote est une molécule particulièrement stable, diamagnétique, et ne réagit pratiquement pas. Mais autour de nous, l’oxygène est lié à pratiquement tous les autres éléments chimiques. Avec l’hydrogène, il forme de l’eau, H₂O, avec le carbone, les hydrocarbures ou les sucres, il forme le dioxyde de carbone et de l’eau. Avec les métaux, il forme les oxydes. Pourtant les êtres vivants, végétaux ou animaux, baignent dans une atmosphère de dioxygène sans réagir violemment (heureusement, sinon nous serions réduits à un peu de dioxyde de carbone, d’eau, de phosphates et d’oxydes métalliques, état thermodynamiquement stable des composantes du corps humain). Au contraire, dans les poumons, le dioxygène se fixe sur l’hémoglobine. Il est le comburant des réactions lentes d’oxydation au niveau des muscles et des tissus. Nous devons cette situation au fait que le dioxygène est paramagnétique et que ses réactions avec des composés diamagnétiques sont lentes. Elles ne se produisent qu’en chauffant, dans une flamme ou grâce à des machines moléculaires complexes comme l´hémoglobine. Nous n’existons donc, loin de la situation d’équilibre thermodynamique que grâce aux propriétés magnétiques du dioxygène …
Que se passe-t-il quand deux électrons du dioxygène se placent dans une même orbitale (Figure 12e) ? Le dioxygène singulet est une espèce excitée qui est produite notamment par la réaction chimique de l’eau oxygénée, H₂O₂, avec des oxydants en milieu basique. Une fois produit, le dioxygène singulet peut se désexciter pour redonner le dioxygène triplet, avec émission d’une belle lumière rouge ou bien réagir avec d’autres molécules qui peuvent à leur tour émettre de la lumière. C’est le cas du luminol et d’autres molécules luminescentes, comme le montre la figure 13. La lumière émise par le ver luisant, rencontré en été au creux des chemins, est produite par cette réaction. De manière plus prosaïque, les marchands de matériel de camping vendent des bâtons lumineux de diverses couleurs et de diverses intensités lumineuses comme sources de lumière de secours. Les colliers lumineux utilisés lors des soirées dansantes de l’été sont basés sur le même phénomène. La réactivité du dioxygène à l’état singulet est ainsi complètement différente de celle du dioxygène triplet.
O₂ singulet (excité) ==> O₂ triplet (stable) + énergie lumineuse (rouge)
O₂ singulet + luminol ==> Espèces excitées du luminol ==> lumière

Figure 13 : Réactivité du dioxygène singulet : produit au cours d’une réaction chimiluminescente, il peut réagir avec des molécules comme le luminol (a) dont les états excités (b) se désexcitent en émettant de la lumière (c).

Radicaux moléculaires
La molécule de monoxyde de carbone NO (figure 12c) est un exemple de radical moléculaire stable : une molécule portant un spin S=1/2. Il y a bien d’autres exemples. Par exemple NO peut réagir avec le dioxygène pour donner le dioxyde d’azote NO₂, également paramagnétique (figure 14c). De nombreuses molécules organiques appartiennent à cette catégorie, par exemple les radicaux nitronylnitroxydes (figure 14d). Dans tous les cas, l’électron célibataire se situe dans une orbitale « frontière », haute en énergie non liante ou antiliante : les électrons « magnétiques » ne participent pas aux liaisons et à la stabilité de la molécule.

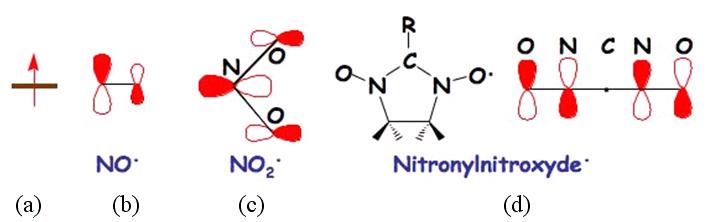
Figure 14 : Quelques molécules radicalaires paramagnétiques et les orbitales moléculaires occupées par un seul électron :
(a) niveau simplement occupé ; (b) NO^• ; (c)NO₂^• ; (d) nitronylnitroxyde^•.

Nous pouvons désormais aborder le sujet essentiel de notre propos : comment les chimistes, connaissant les règles qui régissent l’interaction entre électrons peuvent manipuler les spins des molécules pour obtenir les matériaux magnétiques qu’ils souhaitent ? On comprend que cela ne soit pas si simple car il faut à la fois obtenir des molécules stables, donc former des liaisons solides et garder des électrons célibataires « magnétiques » et contrôler les interactions entre eux, qui sont très faibles (figure 15) ! Si l’on utilise les électrons célibataires pour former des liaisons, on obtient des composés diamagnétiques ! C’est ce qui se passe lorsque l’on fait réagir deux molécules de dioxyde d’azote NO₂ entre elles. Chacune porte un électron. La molécule N₂O₄ qui se forme est diamagnétique. On peut facilement visualiser cette réaction car le dioxyde d’azote est brun (on le connaît souvent sous le nom de vapeurs rousses) et la molécule dimère est incolore. La réaction, qui dégage de la chaleur, est facilement réalisée en baissant la température (figure 16). Elle est réversible : quand on réchauffe, on retrouve les vapeurs rousses de dioxyde d’azote.

Figure 15 : Le dilemme à résoudre : former des liaisons solides avec des électrons organisés en paires diamagnétiques et sauvegarder des électrons célibataires, en contrôlant l’interaction très faible entre eux (avec les images d’un lien familial fort et de Michel-Ange – Chapelle Sixtine, Rome).

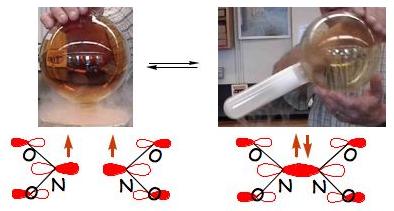
Figure 16 : La réaction de dimérisation du dioxyde d’azote paramagnétique NO₂, brun, à gauche, est favorisée à basse température. Elle conduit à la formation d’une molécule diamagnétique, N₂O₄ incolore, à droite. Sous les photographies, est indiquée l’interprétation orbitale de la formation de la liaison.

Les complexes des éléments de transition
Les éléments de transition sont les éléments de la classification périodique (Figure 17) qui possèdent des orbitales d partiellement occupées par des électrons.

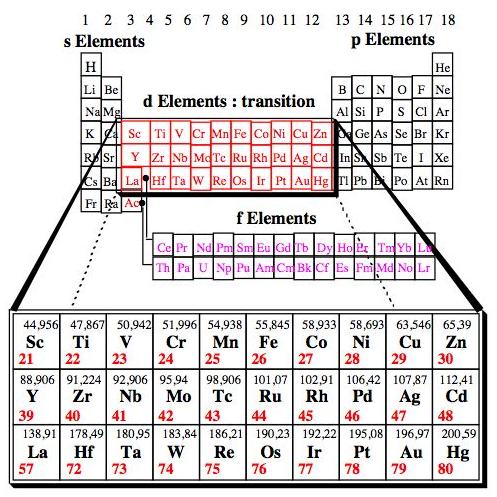
Figure 17 : Classification périodique des éléments mettant en évidence les colonnes 1 à 18,
les éléments s et p et les éléments de transition d

Il y a cinq orbitales d (caractérisées par le nombre quantique l=2), ce qui permet d’obtenir des spins de S=0 à S=5/2 : l’ion manganèse(II), Mn²⁺ ou Mn(II), l’ion ferrique, Fe³⁺ ou Fe(III) ont un spin S=5/2 (figure 18). D’autres éléments, les lanthanides, présentent des orbitales f partiellement occupées au nombre de sept (l =3) et l’on peut obtenir ainsi un spin S=7/2, avec l'ion gadolinium(III), Gd³⁺ ou Gd(III). Dans un ion de transition isolé, les orbitales d ont la même énergie. On dit qu’elles ont dégénérées.

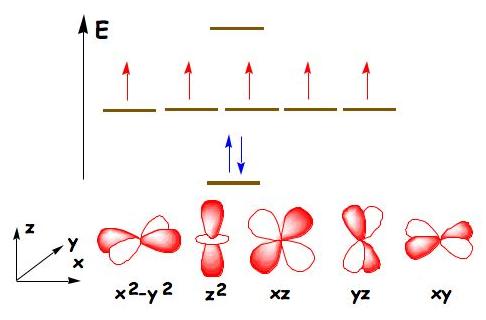
Figure 18 : Les orbitales d des éléments de transition sont à l’origine des propriétés magnétiques, électriques et optiques de ces éléments et de leurs composés. Elles sont de symétrie paire (g). L’exemple correspond à un ion Mn(II) ou Fer(III), spin S= 5/2.

Les ions de transition peuvent s’entourer de molécules que l’on appelle pour la circonstance des ligands (qui se lient, du latin ligare) pour former des molécules plus grandes, appelées des complexes métalliques. L’interaction électrostatique avec les liaisons qui se créent entre l’ion et les ligands est appelée « champ des ligands ». La théorie du champ des ligands est une application extrêmement riche et utile de la mécanique quantique et de la théorie de la symétrie à l’étude de ces complexes. Pour notre propos, il suffit de savoir que l’approche des ligands modifie l’énergie des orbitales métalliques de manière différenciée et que se forment des orbitales moléculaires par combinaison des orbitales du métal et des ligands … Les électrons célibataires se distribuent dans les nouveaux niveaux d’énergie ainsi créés. Pour un complexe octaédrique ML6 où les ligands L forment un octaèdre autour de l’ion métallique M, les orbitales se scindent en deux groupes appelés t_2g et e_g selon des appellations de la théorie de la symétrie (figures 19 et 20).

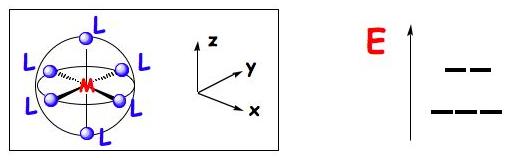
Figure 19 : Modification de l’énergie des niveaux d par un champ des ligands octaédrique.

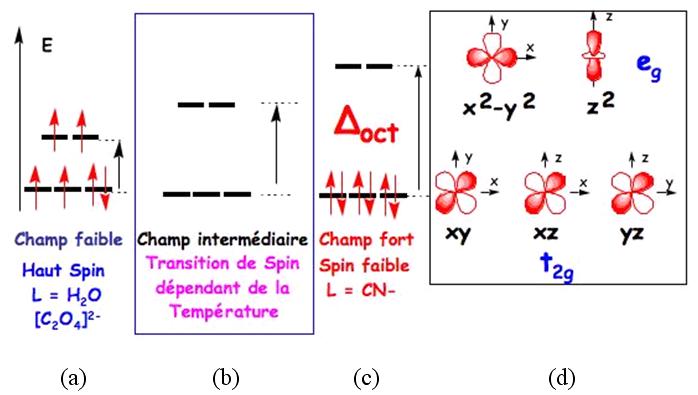
Figure 20 : Orbitales d, t_2g et e_g (en d) ; variation du champ des ligands avec la nature des ligands et influence sur les propriétés magnétiques (a-c).

L’écart en énergie entre les niveaux t_2g et e_g , appelé , dépend de la nature des ligands.

La distribution des électrons dans les niveaux est appelée configuration électronique. L’occupation des orbitales dépend de la nature des ligands et de l’importance du champ des ligands. La figure 20 montre les deux manières de distribuer les électrons dans les orbitales des complexes octaédriques de l’ion fer(II), avec six électrons dans les orbitales d, d⁶. Dans un champ des ligands faible, dans l’ion hexaaqua fer(II) [Fe(II)(H₂O)₆]²⁺par exemple (fig. 20a), les cinq premiers électrons occupent d’abord tous les niveaux disponibles et le sixième électron s’apparie dans une des orbitales t_2g. On obtient un spin S=2 (spin fort ou haut spin). Si l’on remplace l’eau par l’ion cyanure CN^- , lié par le carbone, on obtient un complexe hexacyanoferrate(II), [Fe(II)(CN)₆ ]^4-, où le champ des ligands est très fort, est très important et dès le quatrième électron, les électrons s’apparient dans les orbitales les plus basses en énergie (fig. 20c). Tous les électrons sont appariés. Le spin du complexe est S=0 (spin faible ou bas spin). En enlevant un électron, on obtiendrait un ion fer(III) trivalent, avec cinq électrons dans les orbitales d, d⁵. En champ faible, dans [Fe(H₂O)₆]³⁺ par exemple, le spin est 5/2 et en champ fort, [Fe(III)(CN)₆ ]^3-, le spin est ½. Lorsque le champ des ligands est intermédiaire, intervient une situation extrêmement intéressante où la population des orbitales peut varier en fonction de la température ou de la pression … ce qui donne lieu au phénomène de transition de spin.

Les couleurs des complexes des éléments de transition

La couleur des complexes dans l’eau (figure 21) est une des manifestations de la présence du champ des ligands, qui varie avec les ions métalliques. La couleur des solutions reflète l’écart en énergie entre les orbitales t_2g et e_g et, très exactement, la différence d’énergie entre les deux configurations a) et b) de la figure (figure 22) :
a) état fondamental ; b) état excité par l’absorption d’un photon hv. Les couleurs ne sont pas très intenses car les transitions sont interdites par la symétrie. Les transitions qui exigent un renversement du spin [cas du Mn(II)] sont aussi interdites de spin et deviennent extrêmement faibles comme le montre la couleur très peu intense d’une solution de Mn(II). En outre, la solution d’ions zinc(II) est incolore car toutes les orbitales d sont occupées (configuration électronique d¹⁰).

Figure 21 : Variation de la couleur de solutions aqueuses d’ions divalents de la première ligne des éléments de transition de la classification périodique, du vanadium(II) au zinc(II). La couleur varie avec le nombre d’électrons dans les orbitales d. Les couleurs sont peu intenses car les transitions entre orbitales d dans un complexe octaédrique sont « interdites ».

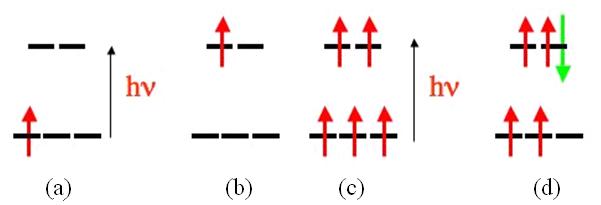
Figure 22 : Schémas de transitions électroniques entre orbitales d des complexes d’éléments de transition : état fondamental d’un complexe d1 ; (b) état excité après absorption d’un photon, sans changement de spin : (c) état fondamental d’un complexe d5 ; (d) état excité après absorption d’un photon : il a été nécessaire de renverser un spin, la transition est fortement interdite. Observer la couleur très pâle de la solution de manganèse(II) sur la figure 21.

Les propriétés magnétiques des complexes des éléments de transition

Il est évidemment possible de mesurer le magnétisme d’une substance avec des balances ou des instruments plus complexes, susceptomètres ou magnétomètres. La figure 23a montre la balance magnétique conçue et utilisée par Pierre Curie. On peut avoir une idée du nombre d’électrons célibataires d’un complexe métallique de manière plus simple avec le dispositif de la figure 23b. On approche une capsule contenant l’échantillon d’un aimant : l’échantillon est d’autant plus fortement attiré que le nombre d’electrons célibataires est plus grand.

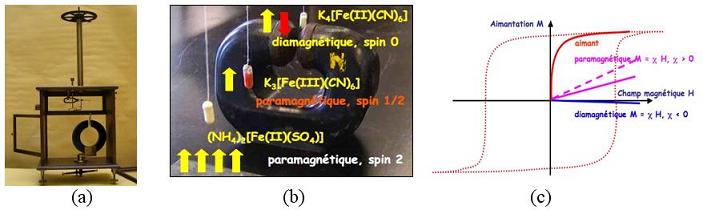
Figure 23 : a) balance magnétique de Pierre Curie (collection de physique, Université Pierre et Marie Curie) ; (b) aimant permanent et échantillons pour montrer que l’aimantation dépend du nombre d’électrons dans des complexes para- ou dia-magnétiques (R. Thompson, Université de British Columbia, Vancouver) ; (c) courbes d’aimantation pour des composés diamagnétique, paramagnétiques, et un aimant.

La manière dont les corps s’aimantent s’appelle l’aimantation M. Dans les cas simples, elle est proportionnelle au champ magnétique appliqué H. La constante de proportionnalité, pour une mole de matière, s’appelle la susceptibilité magnétique

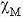
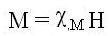[1]

Les substances diamagnétiques ont une susceptibilité magnétique très faible et négative, due aux électrons appariés. Dans les cas très simples de composés paramagnétiques, la susceptibilité magnétique 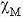dépend du nombre n d’électrons célibataires dans une molécule du composé de la manière, donnée par la loi établie par Pierre Curie (et connue sous le nom de loi de Curie) que l’on peut écrire :

[2]

Avec le système d’unités utilisé ici (dit uem-cgs), la susceptibilité est exprimée en cm³ mol^-1.
Ainsi, sur la figure 23, un échantillon de fer(II) bas spin, contenant [Fe(II)(CN)₆ ]^4-, S=0, où tous les électrons sont appariés, est faiblement repoussé (figure 23c, courbe bleue). Un échantillon de fer(III), contenant [Fe(III)(CN)₆ ]^3-, S=1/2, avec un seul électron célibataire est moins attiré qu’un échantillon de fer(II) haut spin, contenant [Fe(II)(H₂O)₆]²⁺, S =2, avec 4 électrons célibataires (figure 23c, courbes violettes de pente différente). On observe aussi le comportement d’un aimant « dur » (courbe rouge) qui n’obéit pas à la loi de Curie. La pente de la courbe de première aimantation est très élevée puis on obtient un cycle d’hystérésis (du grec husterein, être en retard) quand on fait varier le champ autour de la valeur zéro avec une forte aimantation rémanente (à champ nul) et un fort champ coercitif (champ où l’on retrouve une aimantation nulle). On observe qu’à champ nul, le système est bistable, l’aimantation peut être positive ou négative. Le système a une mémoire et peut être utilisé pour stocker de l’information …

Comment les chimistes peuvent et savent varier les propriétés magnétiques ?

On peut changer les propriétés magnétiques des complexes des éléments de transition, simplement en variant les ligands autour de l’ion métallique. Une expérience simple illustrant la flexibilité de cette chimie est montrée sur la figure 24 : il est possible simplement de changer les ligands, la couleur, la géométrie.

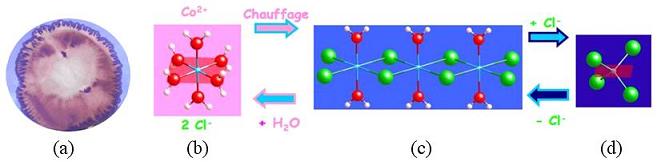
Figure 24 : Flexibilité de l’environnement (sphère de coordination) des ions de transition, cas d’un complexe de cobalt(II) :
(a) Expérience ; (b-c) transformations de l’environnement de l’ion cobalt.

Changement de ligands et de géométrie
Un papier-filtre est imprégné d’une solution concentrée de chlorure de cobalt, CoCl₂, 6H₂O : le papier devient rose pâle [Co(II)(H₂O)₆]²⁺ (figure 24b). Le papier est alors chauffé à l’aide d’un générateur d’air chaud (sèche-cheveux…). Le papier sec devient bleu clair. Il se forme la chaîne de la figure 24c où deux ions chlorure Cl- relient deux ions cobalt. Deux molécules d’eau restent au-dessus et au-dessous du ruban de la chaîne. Cette réaction chimique est parfois utilisée pour donner une indication sommaire du degré hygrométrique d’une atmosphère. Le phénomène est en effet réversible : l’addition de quelques gouttes d’eau (ou une atmosphère humide) permet de revenir à la couleur rose. Cependant, on observe aussi la formation d’une autre espèce bleu violet intense tétraédrique, [Co(II)(Cl)₄]^2- sur les parties du papier où s’accumulent les ions chlorure. La couleur est plus intense parce que le tétraèdre ne présente pas de centre d’inversion et que les transitions électroniques deviennent permises par symétrie (figure 24d). On observe la couleur bleu foncé à la limite des zones rose et bleu clair, où s’accumulent les ions chlorure. Cependant, dans cette suite de réactions, le spin des complexes est resté le même.

Changements de spin
Il en va différemment dans ce qui suit (expérience de la figure 25). Dans une boîte de Petri en verre transparent (pour pouvoir projeter sur un rétroprojecteur), on place une solution diluée de sel de Mohr qui contient l’espèce octaédrique [Fe(II)(H₂O)₆]²⁺, spin S=2.

On ajoute alors une goutte ou deux d’une solution dans l’alcool (éthanol) d’orthophénantroline (o-phen) une molécule organique possédant deux atomes d’azote susceptible de se lier à l’ion fer(II). On observe immédiatement une intense coloration rouge due au complexe [Fe(II)(o-phen)₃]²⁺ représenté sur la figure 25. Le champ des ligands des trois molécules d’ortho-phénantroline est fort et le nouveau complexe a un spin faible, S=0. On remarque (figure 25b) que les trois molécules d’ortho-phénantroline forment une hélice, qui peut tourner à droite ou à gauche : les deux hélices ne sont pas superposables – comme deux mains, droite et gauche - : ces complexes sont chiraux.

Figure 25 : (a) Contrôle du magnétisme (état de spin) d’un complexe métallique de fer(II) à l’aide des ligands : du haut spin à bas spin en substituant des molécules d’eau (complexe vert clair) par des molécules d’ortho-phénantroline (complexe rouge) ; (b) les complexes formés sont un mélange d’espèces chirales ; (c) à l’image de P. Langevin, le chimiste joint l’action à la pensée : ayant compris la nature du champ des ligands, il agit pour changer les propriétés (Paul Langevin, La pensée et l’action, Editions Sociales, Paris).

Les complexes à transition de spin : du quantique au démonstrateur

L’immensité du choix de ligands permis par la chimie organique autorise de réaliser une situation intermédiaire où le champ des ligands présente une valeur moyenne : certains complexes sont haut spin à haute température et deviennent bas spin à basse température. Et ils changent de couleur avec le champ des ligands ! La figure 26a représente la structure schématique d’une chaîne d’ions fer(II) liés par trois molécules neutres de triazole substituées par un groupement R. L’unité de base de la chaîne porte les deux charges positives de l’ion fer(II). Des ions négatifs (anions) se placent entre les chaînes et assurent l’électroneutralité du composé. A haute température, le composé est blanc et haut spin (S=2) ; à basse température, le complexe est rouge bordeaux et bas spin (S=0). Quand le chimiste varie les conditions de synthèse, les substituants R et les anions, il est possible d’obtenir la courbe de susceptibilité de la figure 26b (on peut vérifier les valeurs de 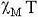pour n = 0 et 2 grâce à la formule [2] …). L’important ici est non seulement le passage de la forme haut spin HS à la forme bas spin BS (BS<==HS) quand on descend en température aux environs de la température ambiante (300K) et inversement (BS==>HS) quand on monte en température, mais le fait que la température de transition est différente . Ce phénomène est appelé « hystérésis ». Il est dû à l’interaction entre les chaînes dans la structure. Il est à la source d’une importante propriété du système que l’on appelle la bistabilité : à une température comprise entre, le système peut être haut spin ou bas spin, blanc quand il vient des hautes températures ou rouge quand il vient des basses températures : il se « rappelle » son passé thermique, il a une « mémoire ». Cette propriété peut être utilisé dans les démonstrateurs d’affichage montrés sur la figure 26b. Des éléments chauffants (par effet Joule) ou réfrigérants (par effet Peltier) permettent l’affichage de plots de couleur différente utilisés dans l’affichage (panneaux d’affichage, carte téléphonique…).
Cet exemple montre le passage de l’utilisation de la mécanique quantique et de la thermodymanique aux propriétés physiques et aux applications.

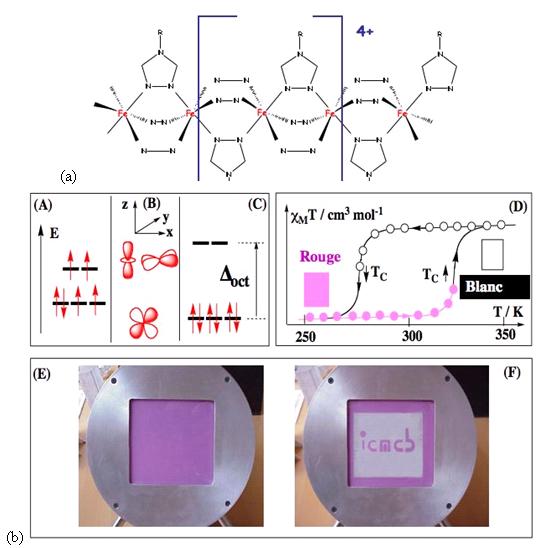
Figure 26 : (a) Structure schématique de la chaîne de fer(II) à ponts triazole, à transition de spin ;
(b) du quantique au dispositif : (A-C) orbitales et états de spin du fer(II) ;
(D) courbe de susceptibilité magnétique et bistabilité du système ;
(E-F) dispositif d’affichage (J.F. Letard, ICMC Bordeaux)

Interaction entre électrons sur des centres voisins : de la molécule à l’aimant

Spins parallèles ou antiparallèles : comment ?
Jusqu’à présent, nous n’avons évoqué que des exemples où les propriétés ne dépendaient que d’ions de transition isolés. Même quand nous avons évoqué des chaînes, les propriétés magnétiques ne reposaient pas essentiellement sur l'interaction avec les électrons sur des sites voisins. Nous franchissons donc un pas nouveau dans la complexité en abordant l’interaction d’échange, qui est une interaction électrostatique, quantique, entre deux électrons portés sur des sites voisins. Une fois encore, nous devons simplifier beaucoup. Nous devons, de fait, trouver le moyen de maîtriser l’interaction pour que deux électrons sur des centres voisins aient leurs spins soit parallèles 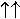(situation de triplet. S=1), soit antiparallèles (situation de singulet, S=0) ! Lorsque les électrons sont localisés, quand ils n’ont pas tendance à sauter d’un centre à un autre, la situation peut être résumée par la figure 27. La différence entre l’énergie du singulet E_S et celle du triplet E_T est la constante de couplage entre les spins. On l’appelle J (= E_S -E_T). Si l’on veut que le triplet soit l’état fondamental, J doit être positif. On dit alors que le couplage est ferromagnétique. Si l’on veut que le singulet soit l’état fondamental, J doit être négatif. On dit que le couplage est antiferromagnétique. A cette « stratégie de spin » correspond une « stratégie orbitale » que nous avons déjà entr’aperçue : le recouvrement de deux fonctions d’onde conduit à la formation de paire d’électrons (couplage antiferromagnétique, dihydrogène), l’orthogonalité de deux fonctions d’onde conduit au couplage ferromagnétique (dioxygène). Il suffit de généraliser comme l’indiquent les schémas des orbitales de la figure 27. Il existe bien sûr des formules et des modèles quantiques pour rendre cette démonstration quantitative, mais l’approche qualitative est ici suffisante. La stratégie orbitale peut alors déboucher sur le choix de structure et de structure électronique des composants, c’est-à-dire sur une « stratégie chimique ».

Figure 27 : Stratégie de spin et stratégie orbitale : le ferromagnétisme naît de l’orthogonalité des orbitales
et l’antiferromagnétisme provient du recouvrement.

Il est également important de contrôler la valeur de la constante J : le couplage entre ions métalliques libres, sans ligand en pont, serait très faible car les fonctions d’onde décroissent très rapidement. Les ligands pontants jouent donc un très grand rôle. La figure 28a montre le recouvrement entre deux orbitales d permis par un ligand et la figure 28b montre un ion pontant cyanure, CN^- , dissymétrique, entre deux ions métalliques différents. La figure 29 montre la structure et la structure électronique d’un précurseur très utile de matériaux moléculaires magnétiques, un hexacyanochromate. Attention : les ions cyanure peuvent être dangereux par ingestion ou parce qu’ils peuvent donner du cyanure d’hydrogène HCN, gazeux et très toxique. Il faut les manipuler avec précaution.

Figure 28 : (a) Rôle du ligand dans l’interaction ; (b) un exemple de pont linéaire court et dissymétrique, l’ion cyanure.

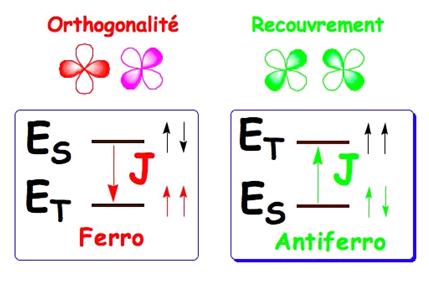
Figure 29 : Structure électronique d’un complexe et rôle du ligand : dans le complexe octaédrique [Cr(III)(CN)₆ ]^3- (a), de spin S=3/2 (b), la fonction d’onde autour de l’ion Cr(III) est très délocalisée sur les ions cyanure (c).

Comment obtenir des molécules à spin élevé ?
Il convient de combiner la stratégie chimique (complexes comportant de nombreux métaux, ou polynucléaires : figure 30), la stratégie de spin (comment a priori combiner les spins ? figure 31), et la stratégie orbitale (pour réaliser les interactions souhaitées).

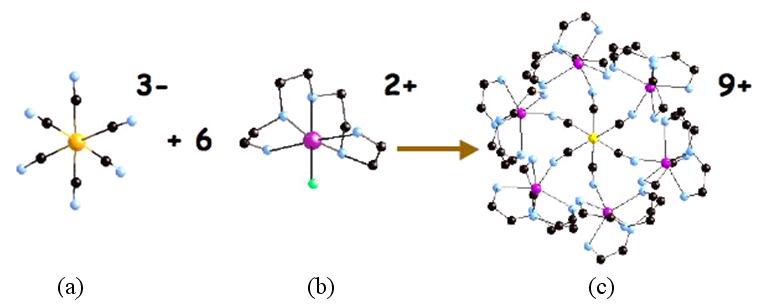
Figure 30 : Stratégie chimique : réaction acide-base pour construire des molécules complexes La réaction de précurseurs simples
[Cr(III)(CN)₆ ]^3-, spin 3/2 (a) et ML²⁺ (spin variable) (b) donne une molécule sphérique [Cr(III)(CN^- ML)₆ ]⁹⁺, en abrégé CrM₆) (c).

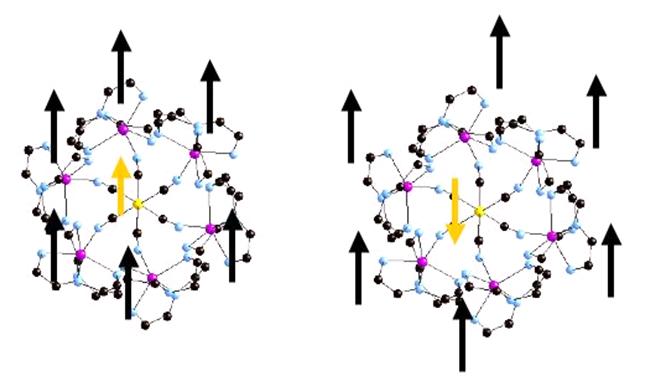
Figure 31 : Stratégie de spin : l’interaction peut être ferromagnétique et tous les spins s’ajoutent (S_A+S_B) ou antiferromagnétique et les spins se retranchent(S_A-S_B). Dans ce dernier cas, quand (S_AS_B), le spin total est non nul et le système est dit ferrimagnétique selon l’expression proposée par Louis Néel.

Les stratégies chimique et de spin sont complétées par la stratégie orbitale : l’orthogonalité crée le ferromagnétisme ; le recouvrement donne naissance à l’antiferromagnétisme. Sans entrer dans le détail, quand dans une molécule CrM₆, on choisit un complexe du nickel(II) (spin 1) comme ion M(II), les orbitales du chrome et du nickel sont orthogonales et le spin du complexe atteint S= 15/2 = 6x1 + 3/2. Si on choisit un complexe du manganèse(II) (spin 5/2), trois des orbitales du chrome et du manganèse se recouvrent, l’antiferromagnétisme l’emporte, le complexe est ferrimagnétique et le spin du complexe, à basse température, atteint S= 27/2 = 6x5/2-3/2. S=15/2 ou 27/2 sont des valeurs qui n’existent pas dans la classification périodique … où le maximum est de 7/2 pour l’ion gadolinium(III) …

Vers des aimants ferro- et ferri-magnétiques à précurseurs moléculaires
Il est désormais possible d’étendre la démarche utilisée de la molécule au solide et essayer d’obtenir des températures d’ordre magnétique aussi élevées que possible. Louis Néel, physicien français, Prix Nobel, a proposé que la température de Curie Tc définie plus haut était proportionnelle au nombre de voisins magnétiques z et à la valeur absolue constante de couplage |J|,alors : .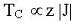

Figure 32 : Formation du bleu de Prusse : (a) réaction chimique ; (b) Structure ; les octaèdres bleus sont les ions [Fe(II)(CN)₆ ]^4- et les sphères jaunes les ions fer(III) ; (c) précipitation progressive dans une boîte de Pétri, à partir de cristaux de ferrocyanure de potassium et de chlorure ferrique(III) placés de part et d’autre de la boîte puis recouverts d’eau. Le précipité se forme là où les solutions entrent en contact par convexion.

Le bleu de Prusse, mis en évidence pour la première fois comme pigment à Berlin, en 1704 par un drapier berlinois du nom de Diesbach, est souvent considéré comme le premier composé connu de chimie de coordination. Il a une structure cubique (les faces des cubes sont également occupées), il comporte des ions fer(II) et fer(III), à deux degrés d’oxydation différents. C’est un composé à valence mixte d’un bleu intense. On le prépare aujourd’hui comme le montre la figure 32. C’est un composé neutre qui compte trois complexes [Fe(II)(CN)₆]^4- pour quatre ions fer(III) : [Fe(III)₄[Fe(II)(CN)₆]₃]⁰. Certains des sites correspondant aux ions ferrocyanure sont vacants et se remplissent de molécules d’eau qui se fixent sur les ions fer(III). Ces lacunes sont très importantes pour les propriétés. Depuis 1704, le bleu de Prusse a fait une belle carrière comme pigment chez les artistes peintres et ailleurs. On peut illustrer cet aspect de sa chimie en réalisant des cyanotypes. Un papier photographique, imprégné d’oxalate ferrique [Fe(III)(C₂O₄ )₃]^3- est recouvert d’un négatif de l’image à reproduire et irradié à la lumière blanche. Aux endroits irradiés, se produit une réaction d’oxydoréduction interne qui transforme le fer(III) en fer(II) et l’oxalate en dioxyde de carbone. On révèle l’image latente, en faisant réagir du ferricyanure de potassium sur le fer(II) formé au cours de l’irradiation (figure 33). Il se forme du bleu de Prusse aux endroits irradiés.

Figure 33 : Préparation d’un cyanotype reproduisant une photographie de Pierre et Marie le jour de leur mariage (original en provenance du musée Curie) : irradiation du papier photographique, bains de révélation, et production de l’image.

Les propriétés magnétiques du composé sont moins exaltantes, c’est un aimant ferromagnétique à la très basse température de 5,6 Kelvins. Un des grands intérêts du bleu de Prusse est sa structure à la fois très simple, cubique d’apparence très rigide, mais de fait très flexible chimiquement : on peut remplacer les ions fe(II) et fer(III) à volonté ou presque et l'on obtient une grande famille d'analogues aux propriétés très diverses. C’est cette flexibilité qui nous a permis de choisir les bonnes paires d’éléments de transition pour créer des interactions ferromagnétiques ou antiferromagnétiques de plus en plus fortes entre voisins métalliques (figure 34), pour obtenir un analogue dont la température de Curie est supérieure à la température ambiante (figure 35).

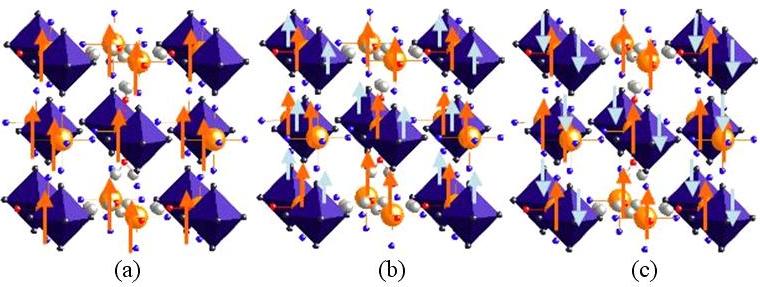
Figure 34 : Orientation des spins dans des analogues du bleu de Prusse dans la phase magnétiquement ordonnée : (a) bleu de Prusse lui-même en dessous de 5,6K ; (b) analogue ferromagnétique : tous les spins sont parallèles ; (c) analogue ferrimagnétique : les spins des plus proches voisins sont antiparallèles. Si les spins voisins sont différents, le spin total est non nul.

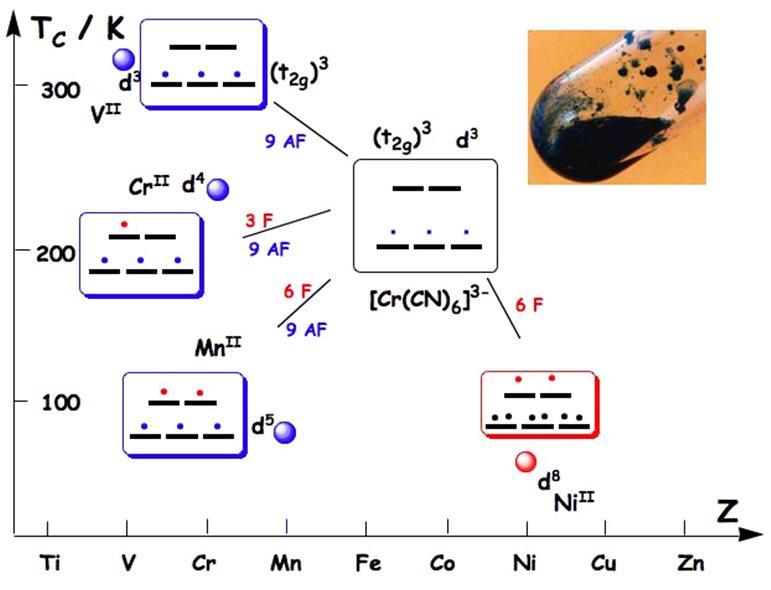
Figure 35 : Diagramme montrant les températures de Curie Tc d’analogues magnétiques du bleu de Prusse de type [A(II)₄[Cr(III)(CN)₆]_8/3] en fonction de la nature et du numéro atomique Z de l’ion métallique A(II) et l’analyse schématique des interactions en compétition (F, ferro, AF, antiferromagnétique). Le dérivé [V(II)₄[Cr(III)(CN)₆ ]_8/3 ]•nH₂O (VCr), est un aimant ferrimagnétique à la température ambiante, d’un bleu profond, transparent, de faible densité (comme le montre l’inséré).

Comme précédemment avec les complexes à transition de spin, on peut utiliser les nouveaux composés ainsi synthétisés pour des applications. C’est ce qui est fait dans les trois démonstrateurs de la figure 36, conçus et réalisés en collaboration avec Gérard Keller (UFR de pharmacie, Université Paris-Sud, Chatenay-Malabry) et F. Tournilhac (ESPCI). Dans les trois cas, le système transite de la phase ordonnée ferrimagnétique à la phase désordonnée paramagnétique à une température proche de l’ambiante (42ºC). Dans les cas (a) et (c), la source d’énergie peut être la lumière (gratuite avec le soleil) et la source froide est l’atmosphère. Dans le cas (b), c’est le milieu ambiant qui est sondé avec une ouverture et fermeture d’un circuit électrique.

Figure 36 : Trois dispositifs utilisant les propriétés de l’aimant à précurseur moléculaire VCr à température de Curie proche de l’ambiante : (a) aimant oscillant, machine thermodynamique transformant l’énergie lumineuse en énergie mécanique ; (b) interrupteur magnétique et sonde thermique ; (c) aimant tournant.

Retour à la molécule isolée, et bienvenue à la molécule-aimant
Un tout autre domaine, particulièrement attractif, s’est développé récemment, celui des molécules-aimants. Il s’agit d’obtenir un solide moléculaire ordonné magnétiquement à grande distance SANS interaction entre les molécules. La figure 37 résume comment cela peut être possible. La barrière d’anisotropie, qui permet au moment magnétique de la molécule de rester dans une direction donnée (donc de garder une information) est d’origine purement moléculaire. Une fois orientée dans une direction, l’aimantation du solide moléculaire relaxe très lentement soit par activation thermique, soit par « effet tunnel » à travers la barrière d’anisotropie. C’est une autre des merveilles de la mécanique quantique, celle de pouvoir franchir des obstacles sans avoir à les sauter.

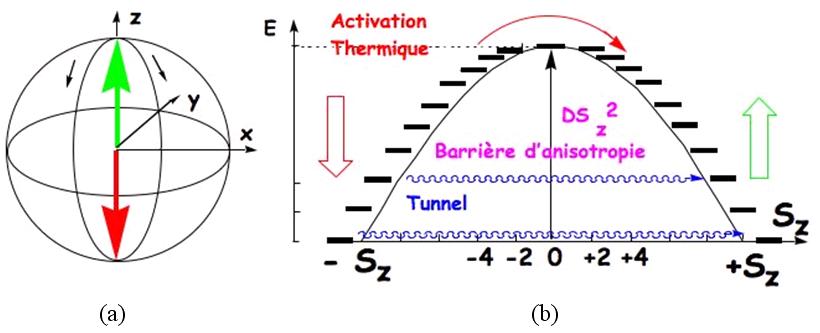
Figure 37 : (a) renversement de l’aimantation dans un système d’anisotropie axiale ; seules sont favorisées les orientations le long de l’axe z, vers le haut (vert) ou vers le bas (rouge) ; (b) un système quantique de spin S élevé, de constante d’anisotropie D négative est doté d’une barrière d’anisotropie de valeur DS² : le renversement de l’aimantation peut se faire soit en chauffant (moyen banal) soit par effet tunnel (voir figure 38b).

La première molécule où a été observé le phénomène a été synthétisée à Wroclaw (Pologne). Elle est représentée sur la figure 38a. Les physiciens lui ont donné « Mn₁₂ » comme nom de bataille. Elle est en effet constituée de 12 ions manganèse, huit ions Mn(III) et quatre ions Mn(IV), liés par des ions oxyde et acétate, qui interagissent pour former un spin S=10 dans l’état fondamental avec une barrière d’anisotropie importante (environ 70K). La courbe d’aimantation en fonction du champ, enregistrée à une température de 2 Kelvins est très remarquable (figure 38b) : elle montre que le cristal moléculaire de Mn₁₂ se comporte comme un aimant classique, très dur, avec une forte rémanence et un fort champ coercitif et dans le même temps, comme un système quantique. Le cycle présente en effet, pour certaines valeurs du champ magnétique, régulièrement espacées, des plateaux et des escaliers qui sont la signature de l’effet tunnel quantique magnétique, observé pour la première fois en 1993 par plusieurs équipes de chercheurs dont celle de Dante Gatteschi (Université de Florence) à qui sont dus ces documents.

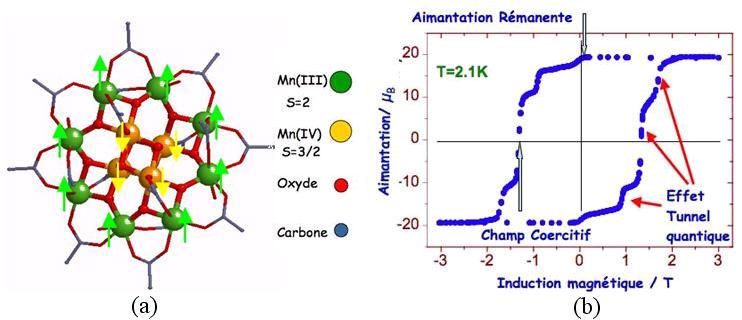
Figure 38 : (a) Structure de la Molécule de « Mn₁₂ » et structure de spin ; (b) Cycle d’hystérésis de « Mn₁₂ » montrant le caractère à la fois classique et quantique du système (communication de D. Gatteschi et R. Sessoli).

Depuis cette date, de nombreux systèmes ont été obtenus qui présentent ces propriétés de relaxation lente de l’aimantation. La courbe de la figure 39b obtenue sur un magnétomètre très sensible, un microSQUID, par W. Wernsdorfer de l’Institut Louis Néel à Grenoble) montre la relaxation lente, variable avec la température, d’une chaîne-aimant synthétisée par R. Lescouëzec (Universitad de Valencia et Université Pierre et Marie Curie).

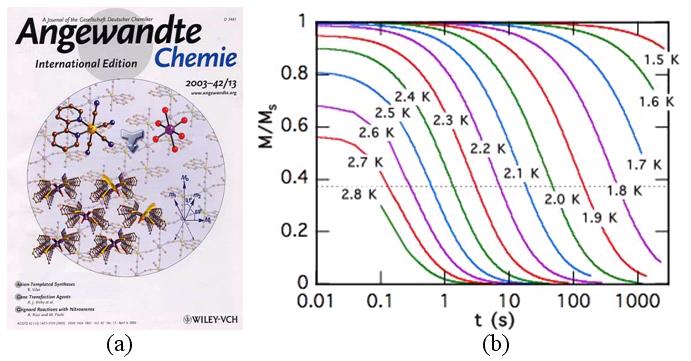
Figure 39 : (a) Couverture d’un journal scientifique européen annonçant l’apparition d’une nouvelle chaîne-aimant ; (b) Relaxation lente de l’aimantation de cette « chaîne-aimant » en fonction de la température (R. Lescouëzec, M. Julve, W. Wernsdorfer).

Ces systèmes ouvrent une voie nouvelle vers le stockage de l’information magnétique à haute densité : il devient possible en effet de rêver de systèmes moléculaires anisotropes à haut spin, assemblés à partir de précurseurs subnanométriques, « à partir du bas » (« bottom up » en anglais), sur lesquels il serait possible de stocker une information sur une molécule UNIQUE, comme le montre le schéma de la figure 40. Le défi est formidable mais c’est un remarquable terrain de travail commun entre chimistes de synthèse, physiciens quanticiens et technologues.

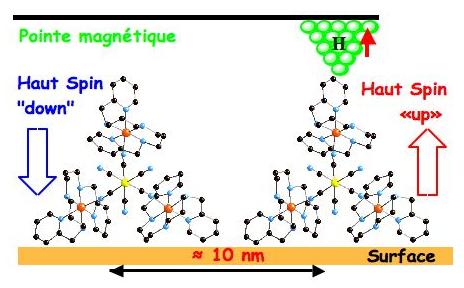
Figure 40 : Un rêve merveilleux : le stockage d’une information magnétique sur UNE molécule, stade ultime de la densité d’information possible. Un ensemble de molécules anisotropes à haut spin refroidies sous champ magnétique alignent leurs moments magnétiques le long de la direction du champ (vers le bas, en bleu). Une pointe magnétique s’approche d’une des molécules et à l’aide d’un très faible champ appliqué retourne l’aimantation d’une seule molécule : un défi pour les chimistes, les physiciens et les ingénieurs illustré avec une molécule « CrNi₃ » bien réelle … (elle a été synthétisée par Valérie Marvaud, Université Pierre et Marie Curie).

Le merveilleux, demain
Nous arrivons au terme de cette brève incursion dans le monde des spins moléculaires qui nous a fait passer du quantique au macroscopique, de la théorie à l’application, de la formule rigoureuse au rêve. C’est un domaine en plein développement qui s’intéresse non seulement au petit, au « nano » mais aussi au complexe. À une époque où tel prix Nobel de Chimie japonais affirme qu’aujourd’hui le chimiste tient à portée de main la synthèse de n’importe quelle molécule, il est tentant de concevoir et de réaliser des systèmes de plus en plus complexes, pour répondre à des besoins nouveaux. Ces systèmes possèdent non plus seulement une propriété ou une fonction choisie, mais plusieurs fonctions : c’est le monde des matériaux multifonctionnels. Ces fonctions peuvent exister côte à côte (magnétisme et transparence) ou elles peuvent interagir l’une sur l’autre, ou les unes sur les autres pour créer et mettre en évidence de nouvelles propriétés. C’est ce qui se produit dans les aimants chiraux que montre la figure 41. Ces aimants sont construits autour de l’une des molécules chirales que nous avons manipulée il y instant en figure 25 avec des ions métalliques choisis comme nous l’avons fait pour les analogues du bleu de Prusse. Ici, le pont entre les ions est un oxalate, le plus simple des diacides carboxyliques organiques [C₂O₄ ]^2-. Comme pour la main, il existe des aimants droits et des aimants gauches, contrôlés par le chimiste…

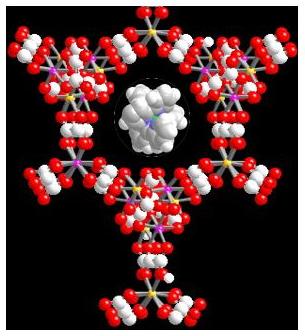
Figure 41 : Aimant chiral (optiquement actif) : un réseau bimétallique tridimensionnel à pont oxalate s’enroule autour d’un précurseur chiral (F. Pointillart, C. Train, M. Gruselle). La présence simultanée des propriétés magnétiques et de chiralité et leur interaction crée une troisième propriété.

Parmi les autres directions riches de développement du magnétisme des systèmes moléculaires, nous terminons (pas encore avec des expériences …) en montrant comment l’irradiation par la lumière peut modifier voire créer les propriétés magnétiques : commutation moléculaire avec formation de spin élevé (figure 42), formation d’un aimant (figure 43a) et commutation rapide à la température ambiante dans un système à transition de spin (figure 43b).

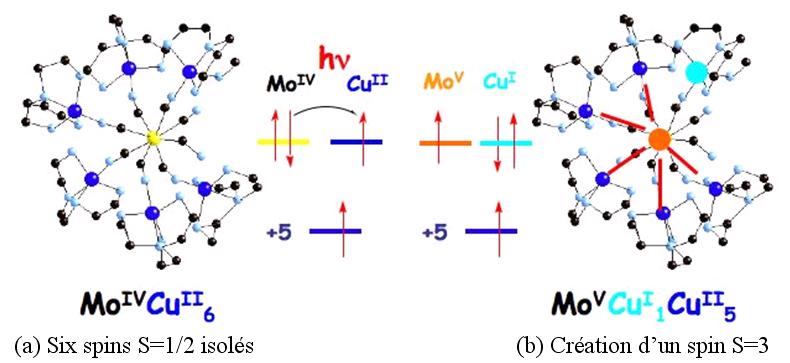
Figure 42 : Une transition électronique transfère un électron d’un atome métallique à un autre dans un complexe, « allume » les interactions d’échange et crée un spin S=3 (J.M. Herrera, V. Marvaud)


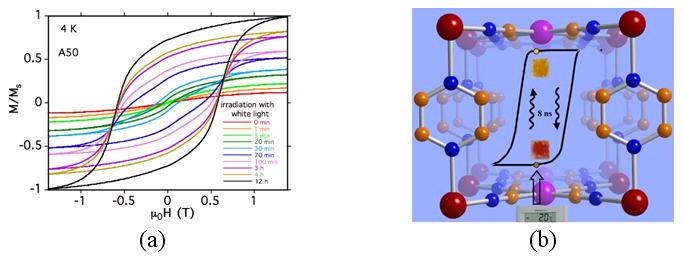
Figure 43 : Deux systèmes photomagnétiques récents : la lumière transforme un analogue du bleu de Prusse à base de cobalt et de fer en aimant (a) (A. Bleuzen et W. Wernsdorfer) et permet une commutation très rapide à la température ambiante entre deux états magnétiques (A. Bousseksou).

Nous souhaitons avoir montré que le monde des molécules magnétiques permet de fournir quelques jolies illustrations pour mieux comprendre, voire démystifier, le magnétisme et ses applications. Nous voudrions également avoir convaincu que le monde du magnétisme moléculaire recèle un potentiel considérable de production de nouveaux objets magnétiques à propriétés prévisibles et modulables, beaux, légers, solubles, faciles à mettre en forme dont certains prendront un jour place dans le vaste ensemble des matériaux utiles dans notre vie de tous les jours.